刘建麟1,2,牛建磊1,3,张宇峰2
(1. 香港理工大学屋宇设备工程学系,香港 2. 华南理工大学亚热带建筑科学国家重点实验室,广州 510640 3. School of Architecture, Design and Planning, The University of Sydney, Sydney, Australia)
摘 要:来流风向与建筑设计对建筑小区内的微气候有重要影响。建筑架空作为亚热带常见的设计之一,已被证明于高密度城市里可改善建筑周围行人区的低风速境况。然而,该设计对局部风环境的影响程度并未深入量化分析。本文通过计算流体CFD,探究四种不同架空高度及三种风向对行人区风环境的影响程度。CFD模拟选用DES模型,并将CFD预测与风洞试验进对比,两者相关系数为0.96。结果表明,建筑侧面高风速区随架空高度与建筑高度比h/H的增大而呈缩小趋势。当来流方向与建筑成90°时,架空下行人区的风速显著偏低,这不利于改善亚热带城区夏季风环境和行人热舒适。
关键词:城市微气候环境;建筑架空设计;DES (detached eddy simulation) 模型;行人区风环境
基金项目:华南理工大学亚热带建筑科学国家重点实验室开放基金资助项目“亚热带城市小区室外风环境和热舒适实测及空间相关分析研究”(2016ZB04)。
0 引言
随着建设宜居城市理念的普及,城镇居民渴望生活在更为舒适的城市微气候环境中来参与户外游憩活动,如散步,太极和广场舞等,这在行人高度区更为重要。建筑物的架空设计,可营造出一层开放空间任由自然风通过,并为二层居住区隔绝热湿,该设计形式被广泛用于我国华南地区及东南亚国家的亚热带城市中。在研究上,Niu等[1]通过夏季调查发现,建筑架空设计在高密度的中心城区能起到良好的局部遮阳和通风作用,并能有效调节其周边的热舒适性。然而在冬季,由于城市主导风向的改变,该架空建筑周围的热舒适性也会发生变化[2]。近期,Liu等[3]和Du等[4]针对某架空设计进行一系列的数值模拟试验分析,得出该设计可作为一种有效方式用于改善建筑周围行人高度的局部微气候环境。然而,当架空高度和来流风向改变时,该设计对行人区域局部流场和热舒适性的影响程度并未得到深入量化地研究。计算流体动力学(CFD)作为研究建筑环境的有效手段常用于城市微气候环境的预测,其核心在于湍流模型的合理选取。近年来,比雷诺时均方法(RANS)更为精确的湍流模型逐渐被研究者用于建筑物绕流的预测中,包括非稳态雷诺模型(unsteady-RANS,URANS),大涡模拟(large eddy simulation, LES)以及复合前两者预测模式的detached eddy simulation(DES)。然而,在应用上,LES需要远高于RANS模型的计算所需内存及计算时间,故而在室外微气候环境的实际预测工程中还未广泛应用[5]。DES作为一种复合模型,其优势在于同时具备了LES的预测准确性和RANS的省时性[3]。文中将选取DES模型用于模拟分析。本文选取亚热带城市中典型单栋架空建筑为例,利用CFD方法(选用DES湍流模型)探究四种不同建筑架空高度及三种来流风向对行人区风环境的影响程度。
1 CFD模拟设置
1.1 DES模型设置
DES作为复合URANS和LES的湍流模型,源于Spalart等[6]提出的S-A湍流模型方程。该方程被改进为非稳态模式并将原有的长度尺度d定义为新的长度尺度d̃,d̃=min(d, Cdes Δ),其中,Δ是网格在x、y和z三向上的最大长度,即Δ=max(Δx, Δy, Δz)[6]。在DES中,当d<Δ开启URANS模式,反之d>Δ则选用LES模式。在DES的研究中,最初建立的DES模型中发现了可能导致错误的预测情况,即出现模拟应力损失。该现象的成因是当选用LES模式时,在厚边界层区和狭窄的涡分离区,若设置网格密度不足以准确求解该处的雷诺应力时将给出错误预测[6]。因此,Spalart等[6]将标准DES模型修正为DDES模型(Delayed Detached Eddy Simulation)用于解决求解边界层区域流场出现的问题。类似地,在DDES中,新的尺度变量d̃不仅依赖于网格尺度本身还依赖于流态特性,这使得在大气边界层区维持URANS模式(或推迟启动LES模式)。
1.2 建筑模型参数、边界条件及数值方法
本文采用Xia等[7]的风洞试验中单栋架空建筑模型为例。该试验测试了风流绕过单栋架空建筑时行人高度区的流场分布。图1(a)给出了该架空建筑示意图,左一为单栋架空建筑,原型尺度为25m(D)×75m(W)×50m(H),含有的架空设计包括3根结构支柱,每根为8m×8m×3.5m,相邻两根支柱间距为17.5m。试验模型与建筑原型间比例为1:200。左二是本文所选取的三种来流方向与建筑间角,分别为0°、45°和90°。图1(b)给出了竖直方向上风洞及CFD中无量纲来流风速廓线(u(z)/ur=(z/zr)0.2)及湍流强度分布(I(z))对比,其中在参考高度zr=150m(原型尺度)下的来流参考风速ur为10m/s。风洞试验中,来流位于建筑高度及其相应风速的雷诺数Re为8.2×104,该值大于Meroney[8]的推荐值1.5×104,从而确保了风洞试验结果与雷诺数间的独立性。Irwin探头被置于水平行人区高度(相对高度z/H=0.04)用于流场测试。文中选用30个位于建筑架空周围的测点用于湍流模型的有效性验证。
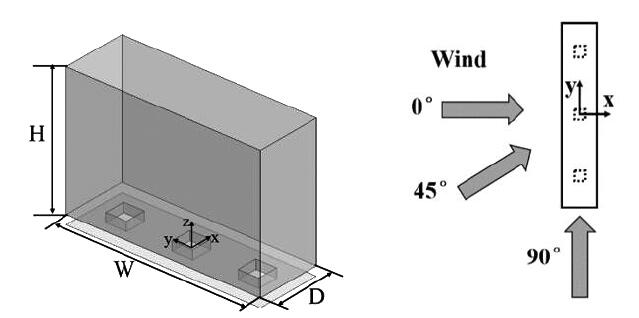 | 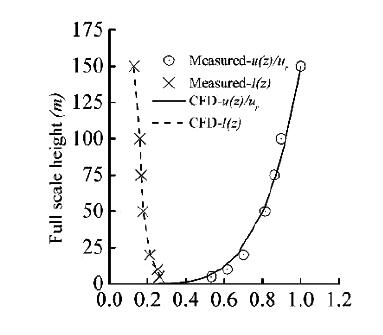 |
| (a)架空建筑模型,来流风向与建筑间角 | (b)入口风速及湍流强度廓线 |
图1 建筑模型及来流风廓线
表1 CFD算例描述
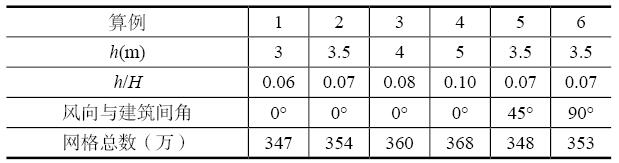
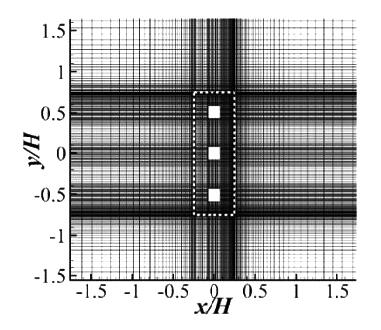
表1给出了本次研究中各算例的建筑架空参数及来流风向设置。结合实际调查,建筑架空高度与建筑高度比(h/H)的范围设定为0.06~0.10。风向选取三组典型风向进行建筑微气候分析。在CFD模拟中,计算空间尺寸设为13.5H×11.5H×6H。该计算空间的壁面距建筑模型的宽和高满足室外风工程模拟导则COST Action 732的推荐值,其横截面比为2.2%也低于推荐值3%[9]。该计算空间采用结构网格(图2)进行划分,根据Spalart针对DES网格假设[10]和作者前期的网格研究[11],为获取精确的流场结果并满足计算网格经济性,在单栋建筑绕流问题中,建筑的迎风面可用较为粗糙的网格(近壁面第一节点y+约为5),建筑侧面、顶面及背风面需采用较细的网格进行划分(y+约为2)。用于DDES模拟设置最小网格尺度为0.0005m,各算例的网格总数列于表1中。其中,参考算例2为354万网格、y+值2.53和计算CFL数1.42。作者在文献[12]中对所采用网格的独立性进行了检验,现有算例中所用网格总数满足当前计算机性能的经济性要求。
 | 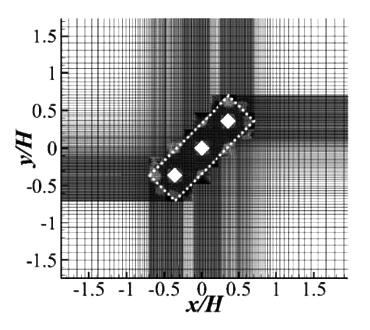 | 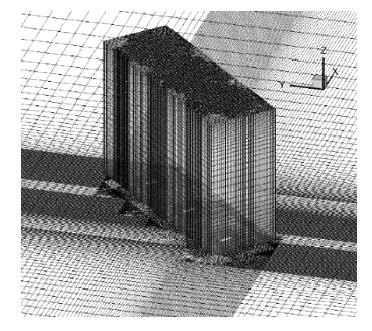 |
| (a) | (b) | (c) |
图2 网格划分:来流风向与建筑物分别呈(a)0°及(b)45°(c)算例5的三维网格视图
入口的边界条件根据风洞试验[7]来流廓线给出,计算的湍动能及扩散率分别为k=1.5(u(z)I(z))2和ε =Cµ0.5kdu/dz。在非稳态的DDES模拟中,来流的湍流脉动特性用涡街法(vortex method)在入口处随机生成190个涡来模拟。计算空间的侧壁和顶部边界设为零梯度条件,地面及建筑壁面设为无滑移边界,出口设为自由出流且保证无回流。计算中所有算例的收敛标准均为各参数达到到残差低于10-4为止。在DES模拟中,离散方法选取PISO算法,对流项和扩散项采用中心差分格式和二阶迎风格式求解。Liu和Niu针对DES模拟单栋建筑绕流问做了相关模拟参数的影响性分析,推荐采用离散时间步长为0.005s,采样计算无量纲时长t*为288(t*=t×ub/b)即真实时间尺度下8s[11]。
2 结果与讨论
2.1 湍流模型的有效性验证
以算例2作参考(图3),将CFD模拟与风洞试验的时间平均风速进行对比,并通过相关性分析进一步评估两者吻合度。
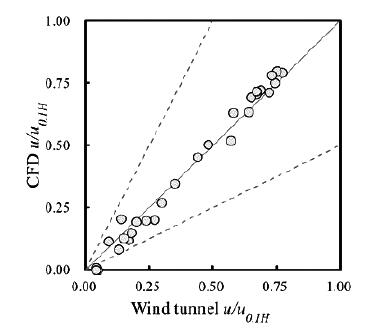
图3 湍流模型及数值方法的有效性验证(CFD结果与风洞试验结果对比)
图3中圆点表示风洞试验结果与CFD模拟结果的对应关系,实线表示y = x,虚线分别指试验值与CFD模拟值间为1:2和2:1关系。公式(1)~(4)用于两组结果的相关性分析,其中,FAC2表示圆点位于1:2和2:1关系之间的百分数,百分数越高指CFD结果越接近试验结果;模拟的偏离程度用无量纲平均偏差(MNMB)表示,其取值为[-2,+2];模拟的总平均偏差用FGE来表征,其区间为[0,2]。当MNMB或FGE取值为0时,均表示最佳预测。相关系数R可进一步评价CFD模拟结果是否与试验结果的趋势一致,其取值介于0和1之间。R越接近1表示CFD结果越趋近于试验结果,反之则偏差越大。



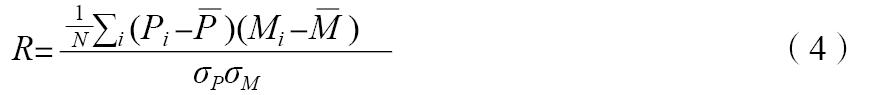
式中:P和M分别为预测值和试验值,指数i = 1,…, N,N为总的试验点个数。通过计算式(1)~ (4),FAC2= 0.92、MNMB= -0.09、FGE= 0.22 和 R= 0.96。结果表明,在采用DDES模型及前文的数值方法进行模拟预测下,来流风向为0°时的CFD模拟与风洞的时均风速吻合度高,该模型与数值方法可用于后续模拟分析。
2.2 架空高度对行人区风环境影响
图4给出在不同架空高度下行人区的无量纲风速场分布。以图4(b)为例,各算例均能准确描绘自然风绕过单栋架空建筑应呈现的基本流态,包括:建筑迎风面的低风速区 (uxy /ur < 0.30)、建筑两侧和架空下方的局部高风速区(> 0.75)和建筑背风面的空气动力学阴影区 (呈低风速)。同时,风能够自由流过建筑物架空下方,并放大其局部风速。对比图4中各图的风速分布,得出建筑物两侧的局部高风速区,随着架空高度的增加呈现高速区域 (橙色) 面积缩减趋势。然而在一定设计高度范围内(h/H=0.06~0.10),仅靠改变建筑架空设计的高度,对建筑物迎风面及建筑物背风面主要区域的速度分布并无较大影响。
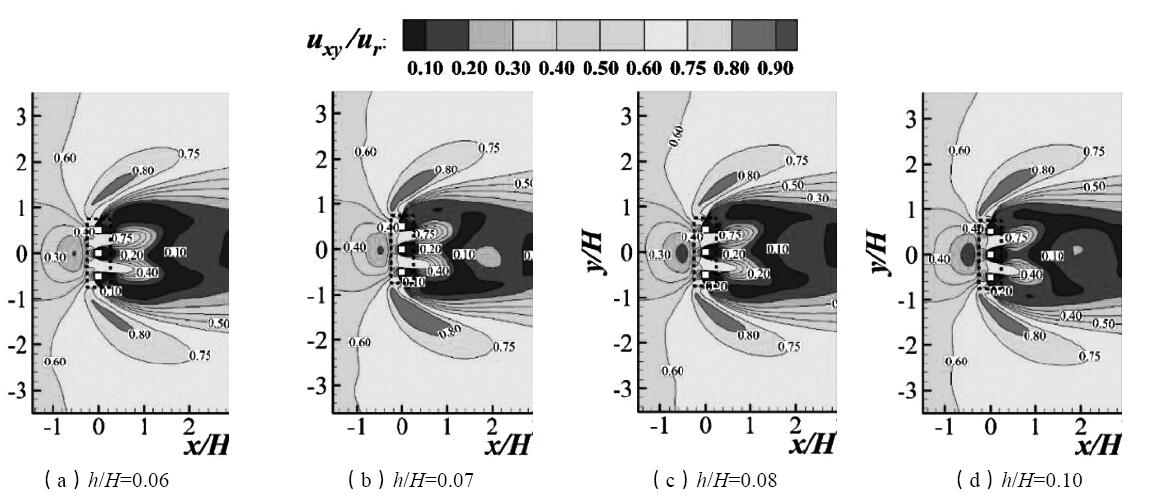
图4 建筑架空设计高度(h/H)对周边行人区域高度下无量纲时均风场的影响
2.3 来流风向对行人区风环境影响
图5和图4(b)分别给出在不同的来流风向下,同一架空建筑周围行人区域的无量纲时均风速场分布。当风向与建筑间角为0°及45°时,建筑两侧仍可见局部高风速区域。同时,对比图4(b)和图5(a)中建筑背风面的空气动力学阴影区,可知其形状变化明显但面积变化较小。当风向与建筑间角为90° 时(图5(b)所示),建筑两侧高风速区域消失,且空气动力学阴影区域面积显著减小。在图4(b)和图5中,原架空下方支柱间的局部风速扩大区随着来流风向从0°、45° 到90°,呈现逐渐减小直至消失的现象,其无量纲平均风速也由0.70降至0.65,最终达到0.10。由此可见,来流风向与建筑间角对架空设计用于改善建筑周围风环境影响显著。在实际设计中,建筑架空虽能有效地改善亚热带地区局部低风速环境和局部热舒适,但当地主导来流风向与建筑间的角度关系也应根据热舒适设计需求做进一步考虑。
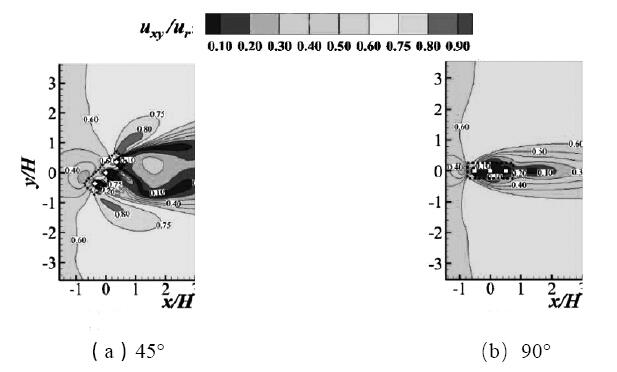
图5 来流风向与建筑间角对周边行人区域高度下无量纲时均风场的影响
3 结论
在亚热带城市小区中,采用DES模型探究了四种不同建筑架空高度和来流风向对架空建筑周围微气候环境及其热舒适性的影响。结果表明:(1) 湍流模型DES能准确预测出架空建筑周围的风环境,与风洞试验结果吻合度高,计算相关系数为0.96;(2) 在相对设计高度h/H = 0.06 ~ 0.10内,仅改变架空高度对建筑物迎风面及背风面主要区域的平均风速分布并无较大影响;(3)来流风向与建筑间角对架空设计用于改善建筑周围风环境影响显著,并且在架空下方支柱间的局部风速扩大区随着来流风向从0°、45° 到90°,呈现逐渐减小直至消失的现象,其无量纲平均风速也由0.70降至0.65,最终达到0.10。本文给出 DES模型用于建筑架空高度设计参数和风向对行人风环境影响的参考,对未来城市通风和微气候设计有指导意义。文中虽采用DES模型对瞬态流场进行模拟计算,但限于篇幅,并未对流场的湍流特性及其对建筑周围瞬时热舒适性做深入分析。同时,设计建筑架空时除应考虑高度外,结构支柱的长宽和形状也值得探究,这都将在后续研究中进一步讨论。
参考文献
[1] NIU J, LIU J, LEE T, et al. A new method to assess spatial variations of outdoor thermal comfort: Onsite monitoring results and implications for precinct planning [J]. Building and Environment, 2015, 91(0):263–270.
[2] LIU J, NIU J. Assessment on seasonal variations of outdoor thermal comfort with on-site monitoring in a precinct [C]// Proceedings of the Urban Transitions Global Summit. Shanghai, China. ELSEVIER, 2016.
[3] LIU J, NIU J, XIA Q. Combining measured thermal parameters and simulated wind velocity to predict outdoor thermal comfort [J]. Building and Environment, 2016, 105(0):185–197.
[4] DU Y, MAK C M, LIU J, et al. Effects of lift-up design on pedestrian level wind comfort in different building configurations under three wind directions [J]. Building and Environment, 2017, 117(0):84–99.
[5] BLOCKEN B, STATHOPOULOS T, VAN BEECK J P A J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment [J]. Building and Environment, 2016, 100(0):50–81.
[6] SPALART P R, DECK S, SHUR M, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities [J]. Theoretical and computational fluid dynamics, 2006, 20(3):181–195.
[7] XIA Q, LIU X, NIU J, et al. Effects of building lift-up design on the wind environment for pedestrians [J]. Indoor and Built Environment, 2015, 0(0):1–18, http://dx.doi.org/10.1177/1420326X15609967 (in press).
[8] MERONEY R N. Wind tunnel and numerical simulation of pollution dispersion: a hybrid approach. Invited Lecture, Croucher Advanced Study Institute on Wind Tunnel Modeling [R]. Hong Kong: Hong Kong University of Science and Technology, 2004.
[9] FRANKE J, HELLSTEN A, SCHLÜNZEN H, et al. Best practice guideline for the CFD simulation of flows in the urban environment [R]. Hamburg: COST Action 732, 2007.
[10] SPALART P R. Young-person’s guide to detached-eddy simulation for bluff bodies [R]. USA: NASA Center for Aerospace Information, 2001.
[11] LIU J, NIU J. CFD simulation of the wind environment around an isolated high-rise building: An evaluation of SRANS, LES and DES models [J]. Building and Environment, 2016, 96(0):9–106.
[12] LIU J, Design for outdoor thermal comfort : on-site monitoring and modeling of airflow in building surroundings [D], Hong Kong: Department of Building Services Engineering, The Hong Kong Polytechnic University, 2017.
注:本文收录于《建筑环境与能源》2017年5月刊总第5期《2017全国通风技术年会论文集》中。
版权归论文作者所有,任何形式转载请联系作者。









