吴文忠
(西安科技大学,陕西西安 710054)
摘 要:烟气压力和温度是高层住宅厨房竖向集中排烟系统的基本参数。住户油烟机开启工况服从泊松过程,驱动竖井内烟气压力和温度变化,因此本研究应用守恒定律和泊松过程知识,首先分析随开启工况变化的排烟中性层高度、竖井出口处烟气压力分布函数,接着分析随开启工况变化的竖井出口处烟气温度分布函数。由这二类分布函数,应用随机分析方法进一步计算任意开启工况下竖井出口处烟气压力和温度。这二类基本参数是排烟系统优化排烟效果和回收利用排烟热量的基础。
关键词:高层住宅;厨房;集中排烟系统;压力;烟气温度;泊松过程
0 引言
厨房排烟中含有CO、CO2、尘埃等有害物质,为了保证厨房清洁,高层住宅设计竖向集中排风系统。龚胜强等[1]模拟了给定开启工况时竖井内静压分布规律,底层压力最大,顶层压力最小,开启率越大,竖井内静压值越大,而且静压值受开启不均匀特性影响。
由于竖井内静压分布总体上自上而下逐渐增大,排烟量则自上而下逐渐减小,低层用户排烟量很低,底层用户排烟量最小。因此高军等[2]在单纯用户动力的基础上,在竖井出口设置排烟风机,和用户抽油烟机构成复合动力系统,获得高效率的排烟效果。
根据我国住宅居住调查:高层住宅楼内同一排风道系统的吸油烟机同时开机率一般在30%~60%之间,多数情况为20%~55%的开机率。
在给定开机率时,排烟参数表现出不均匀性质,有不同的描述参数:龚胜强等[1]定义排烟路径长度描述开启不均匀特性;高军等[2]采用静压方差,皮李[3]采用排气系统不均匀率。
在自然排烟方式下,由于烟囱效应,建筑室内,楼梯间、电梯间、室内和竖井内静压分布存在中性层,向伊依等[3]通过对学生公寓楼和综合楼测试表明了中性层高度和各层静压分布。竖井出口处压力随中性层高度变化,进而影响排烟效果。在排烟系统中,中性层高度影响竖井内静压分布,也影响出口处排烟量。
厨房排烟是燃料燃烧产物,温度高于环境温度,应用热回收节能技术手段,可以节约能源,起到减排的作用,有着积极的社会效益和环境效益[4-5]。
张鑫等[5]为了设计桌面烧烤排气罩,实测烧烤盘加热面温度在180~380℃,与周围空气最大温度差360℃。厨房排烟在竖井出口处温度是设计热回收节能措施的参数。
住户开启排烟是随机事件,服从二项式分布,开启排烟机的累计数量是一个泊松过程。受该过程驱使,集中排烟系统竖井内压力和温度分布呈现随机变化特性,因此本研究应用守恒定律和泊松过程知识[7-9],首先分析随开启工况变化的排烟中性层高度、竖井出口处烟气压力分布函数、竖井出口处烟气温度分布函数。由这二类分布函数,应用微分几何知识[10-12]和随机分析方法[13-14]进一步计算任意开启工况下竖井出口处烟气压力和温度。这二类基本参数是排烟系统优化排烟效果和回收利用排烟热量的基础。
1 排烟工况随机特性
假设某高层住宅有N个住户,每户使用相同抽油烟机,排烟量均为m,排风扇压力均为p,屋顶风机压力pceiling,诱导竖井出口处排烟速度vn。
1.1 开机工况服从泊松分布
考察同一排风道系统的吸油烟机同时开机率:对于一个用户,开机工况有二个:“开机”和“不开机”,服从概率约为1/24(每天开机1h)的二项分布,对于N个住户,开机工况也是服从二项分布,且当住户数充分大而每户开机概率很小(小于0.1)时,该分布近似地表示为λ=N/24
的齐次泊松过程分布函数:
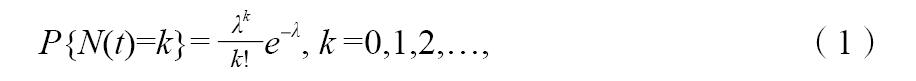
这也是开机率为N(t)/N的概率分布函数。
1.2 排烟工况模拟
已知排烟工况服从泊松过程,设定住户数和考察时间,可以应用Matlab软件对开启过程进行随机模拟。图1是λ=2的开启过程在50s时间内的变化情况。

图1 λ=2的开启过程在50s时间内的变化情况
2 排烟竖井内烟气中性层高度分布函数
高层建筑厨房集中排烟系统,采用变截面或等截面排烟竖井形式,其中等截面排烟竖井形式应用最广,如图2。选取竖井为控制体积。
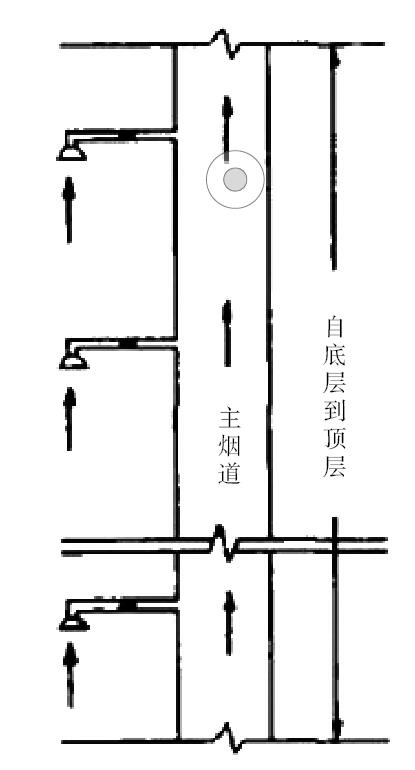
图2 高层建筑厨房等截面竖井集中排烟系统示意图
给定开启工况N(t)=k。选取竖井不同截面,考察排烟机械能守恒。假设用户风机压力仅提供分散排烟动能。下部不开口,仅在竖井出口处开口,出口处没有流动时,中性层在出口处,竖井内部任意高度处静压是负值,即:

当竖井出口处附加屋顶风机时,假设用户风机压力全部转化为烟气动能,则竖井内部中性层不变,仍维持在竖井出口处,即:
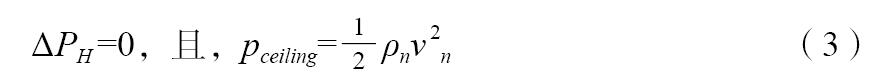
于是在出口处排出烟气量为:

更一般地,当采用混合动力排烟方式时,用户风机、屋顶风机压力均贡献竖井内静压。假设竖井底部内外静压差维持:

则竖井出口处静压差:

忽略不同高度处动能差,则竖井内任意高度处静压差:
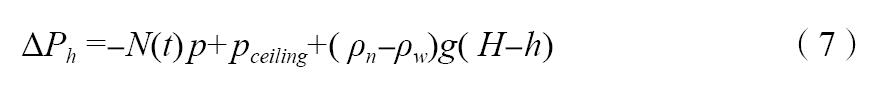
在上式中令ΔPh =0,得到中性层高度:
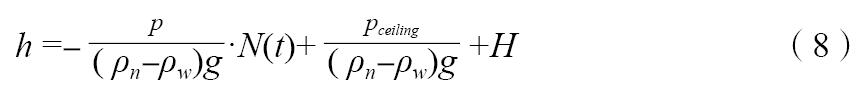
显然,当采用分散动力排烟方式,即pceiling=0时,给定高度h处压力ΔPh的绝对值随开机数量增大而增大;当采用混合动力排烟方式,并保持给定高度h处压力ΔPh不变时,屋顶风机压力pceiling随开机数量增大而增大。
由上式和开机工况分布函数式(1),并记:
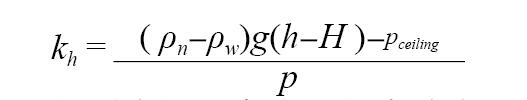
得到中性层高度的概率分布函数为:
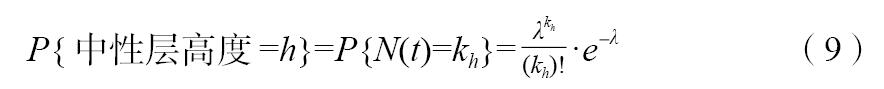
3 竖井出口处烟气参数分布函数
对于同一排风道系统,主要考察竖井出口处参数。该处静压已经由式(6)得到,而且因此得到竖井出口处排烟量:
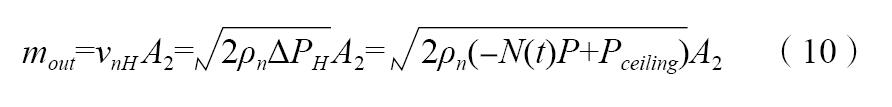
3.1 烟气参数分布函数
在竖井出口处,烟气温度由局部理想气体状态方程和式(6)得到:
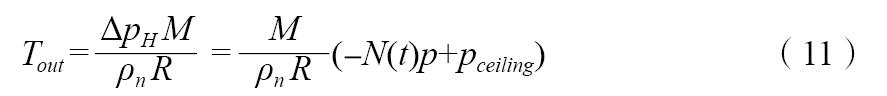
式中:M是烟气摩尔质量,R是理想气体状态常数。
由上式和开机工况分布函数式(1),并记:
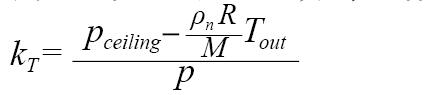
得到出口处排烟温度的概率分布函数为:
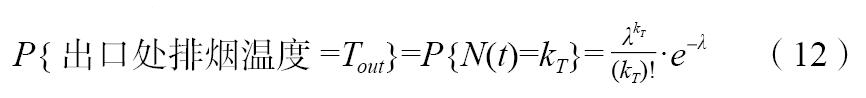
由式(6)和开机工况分布函数式(1),并记:
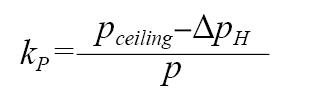
得到出口处排烟温度的概率分布函数为:
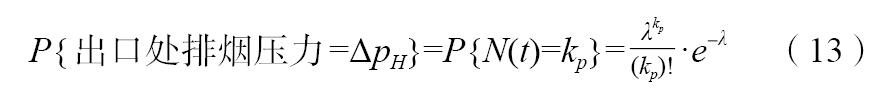
3.2 烟气参数不均匀性质
前文已经得到出口处烟气参数概率分布函数。如果给定开机工况N(t)=k,这些开启楼层位于不同的高度,排烟路径总长度不同,会加剧烟气参数不均匀。已知开机工况服从泊松过程,给定开机工况下排烟路径长度也是随机变量,假设这二个序列相互独立,应用排烟路径总长度变化过程描述排烟参数不均匀性,则该过程是典型的复合泊松过程:

它的数学期望为:
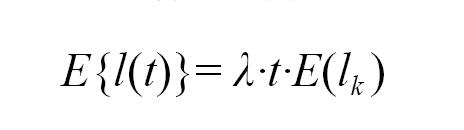
方差为:
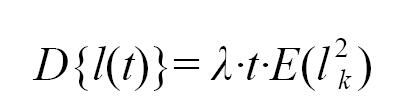
则该不均匀过程的极限分布函数近似为期望为λ·t·E(lk ),方差为λ·t·E(l2k )的正态分布函数:
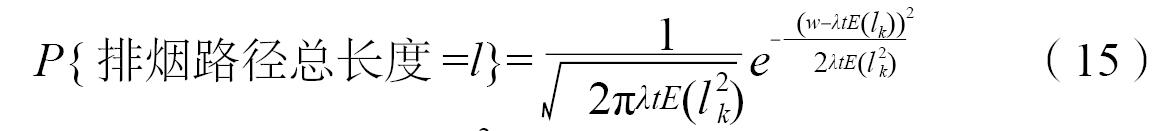
图3是E(lk )=0,λ·E(l2k )=1,t=1s时间内排烟参数不均匀过程模拟情况。
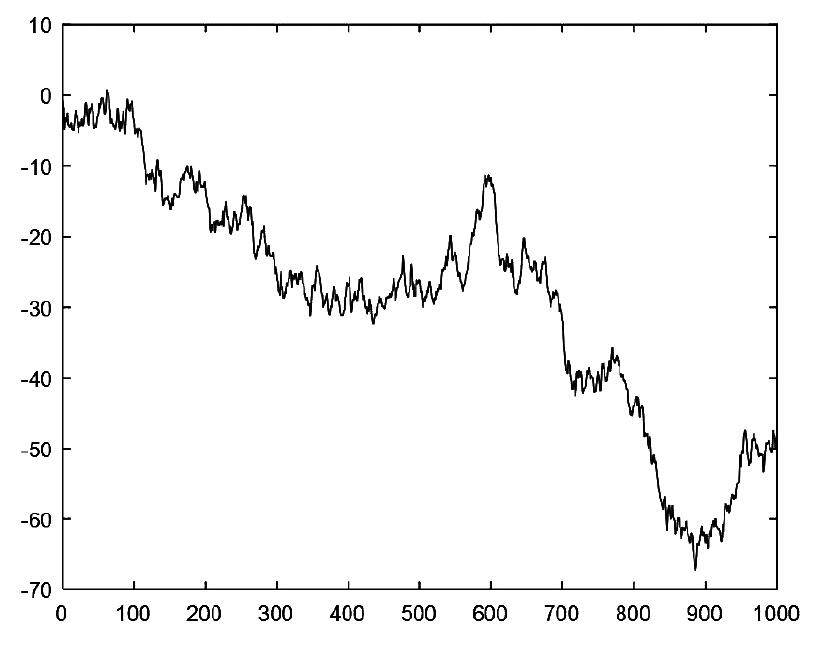
图3 排烟参数不均匀过程模拟
因为给定开机工况时,不同的排烟路径长度也会影响烟气参数,因此根据式(15)修正排烟参数分布函数式(12)和(13)为:


式中:α和β是常数,且α+β=1,最简单取值情况为α=β=1/2。
4 任意开启工况下竖井出口处排烟参数
已知开启工况服从泊松过程,排烟参数不均匀性质近似服从正态分布,按照前述结果可计算竖井出口处排烟参数均值。更细致地,应计算在随机开启工况和不均匀性质条件下排烟参数的条件数学期望。
4.1 排烟条件
开启工况服从泊松分布,分布函数按式(1);不均匀性质近似服从正态分布,分布函数按式(15)。排烟系统处于地面上重力环境中,存在牛顿引力势:
记RN空间内单位球面积为a(N),有:a(2)=2π,a(3)=4π,…,则牛顿引力势核为:
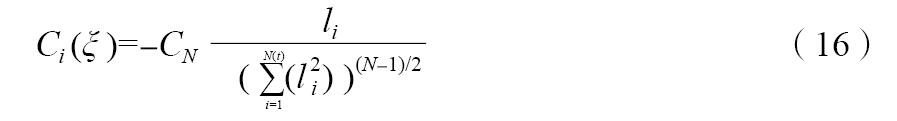
式中:CN = 2(N-2)/a(N ), N > 2。
4.2 排烟参数计算
考察在上述条件下计算竖井出口处排烟参数,则首先需要计算该处排烟参数条件数学期望。记出口处压力和温度的张量仍为[8-10]。由随机分析理论[11-12]得到任意开启工况下出口处烟气压力的条件数学期望为:
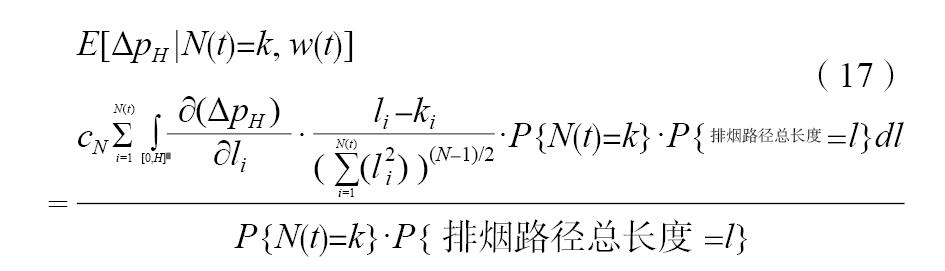
由此得到出口处烟气压力为:
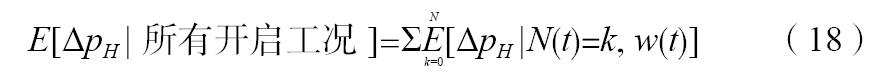
在上式中替换ΔpH为Tout,得到出口处烟气温度。显然,如果不考虑排烟参数的随机特性,即令上式中概率分布函数均等于1,上式就是给定开机工况N(t)=k时竖井出口处烟气压力式(6)和温度(11)。
5 结论
烟气压力和温度是高层住宅厨房竖向集中排烟系统的基本参数,也是排烟系统优化排烟效果和回收利用排烟热量的基础。这二个参数受住户油烟机开启工况的随机特性驱动。
排烟环境中,开启工况服从泊松过程,排烟参数不均匀度以正态分布为极限分布,因此本研究首先推导了开启工况和排烟参数不均匀度概率分布函数,接着应用机械能守恒定律,推导了随开启工况随机特性驱动的排烟中性层高度、竖井出口处烟气压力和温度概率分布函数。为了分析在随机开启工况条件下竖井出口处烟气参数,应用随机分析方法和这二类分布函数,进一步推导了任意开启工况下该处烟气压力和温度的计算公式,它们包含了给定开机工况时竖井出口处烟气参数计算方法。
参考文献
[1] 龚胜强,刘勇,熊健,王振飞,张钰巧. 高层住宅厨房集中排烟系统特性研究 [J].建筑技术开发,2016增刊:173–178.
[2] 高军,丁希晖,陈磊,吴利. 高层住宅厨房复合动力变排风量系统及其特性计算 [C].2016年第二十届全国暖通空调制冷学术年会论文集,目次:138.
[3] 皮李. 高层建筑等截面多动力源排风道流动特性计算与模拟分析 [D]. 西安:西安建筑科技大学,2104.
[4] 向伊依,潘嵩,张健宸,林瑶,程作. 北方地区高层建筑在“烟囱效应”作用下的不同竖井区域压差分布特性及节能策略 [J].建筑技术开发,2016,vol.43(10):41–45.
[5] 刘云祥. 排风热回收系统应用的探讨 [J].暖通空调 HV&AC,2012vol.42(7):72–77.
[6] 张鑫,刘绍忠. 浅谈桌面烧烤排气罩设计 [C].2016年第二十届全国暖通空调制冷学术年会资料集,目次:064.
[7] WU Wen-zhong. Stochastic prediction and control to methane in coalmine [J]. Journal of Coal Science & Engineering (China), 2011,vol.17(3):321–325.
[8] 魏艳华,王丙参,宋立新.复合泊松过程性质及其应用 [J].宜宾学院学报,2009,9 (12):45–48.
[9] 孙天晴.基于复合泊松过程战略石油储备天数的概率模型及其应用 [J].数理统计与管理,2007,26 (5):12–14.
[10] 马力. 简明微分几何 [M]. 北京:清华大学出版社,2004.
[11] 刘连寿,郑小平. 张量分析 [M]. 北京:科学出版社,2008.
[12] 高丽敏,李开泰,刘波,苏剑. 积分守恒型N-S方程通用形式及其在数值模拟中的应用 [J]. 计算物理CHINESE JOURNAL OF COMPUTATIONAL PHYSICS,2008 vol.25(2):172–178.
[13] Paul Malliavin. Stochastic Analysis [M]. Springer-Verlag, berlin, 2006.
[14] Paul Malliavin, Anton Thalmaier. Stochastic Calculus of Variations in Mathematical Finance [M]. Springer-Verlag, berlin, 2006.
注:本文收录于《建筑环境与能源》2017年5月刊总第5期《2017全国通风技术年会论文集》中。
版权归论文作者所有,任何形式转载请联系作者。









