天津科技大学机械工程学院 朱传琪 田玮 张安朝 史佳鑫
天津市建筑设计院 尹宝泉
摘 要:为研究不同输入参数对于办公建筑能耗的影响,并确定办公建筑能耗的概率密度分布,联合使用建筑能耗模拟程序EnergyPlus以及统计学R语言,进行办公建筑能耗的不确定性和敏感性分析。首先通过拉丁超立方法对所研究参数在给定范围内抽样,得到模型输入参数组合,然后利用R语言和EnergyPlus完成数百个模型的自动建模。最后对能耗计算结果进行不确定性分析和敏感性分析。不确定性分析可得到办公建筑取暖、制冷能耗的分布情况,而敏感性分析能确定影响办公建筑的取暖和制冷能耗的主要参数。根据敏感性分析和不确定性分析结果可为新建建筑节能设计及既有建筑节能改造提供指导。
关键词:建筑能耗;自动建模;拉丁超立方抽样;敏感性分析;不确定性分析
基金项目:国家自然科学基金项目(51778416);教育部哲学社会科学研究重大课题攻关项目(16JZD014)。
0 引言
根据《中国建筑能耗研究报告(2017年)》[1],2015年我国建筑能源消费总量为8.57亿吨标准煤,占全国能源消费总量的20%。其中公共建筑能源消费达3.41亿吨标准煤,占全国建筑能源消费总量的39.8%。因此,探究公共建筑能耗特性并提出相应的节能措施,对于降低建筑能耗促进建筑节能发展有重要意义。
由于影响建筑热性能的参数具有很强的不确定性[2],包括人行为、室内得热、建筑围护结构性能参数等。为了达到量化这些参数不确定性的目的,不确定性分析已经广泛应用于建筑能耗分析的各个领域,包括能耗模型校验[3, 4]、生命周期分析[5, 6]、建筑优化改造[7]等。另一方面,敏感性分析可确定影响建筑能耗的主要因素,其中全局敏感性分析法可用于确定建筑能耗输入和输出参数之间的复杂关系,并可考虑变量间的相互作用,所以这种全局性敏感性分析方法引起研究者广泛的兴趣。Patrick等利用敏感性分析方法研究在设计阶段建筑能耗模型中各个参数对建筑能耗的影响[8]。Joseph C·Lam等利用敏感性分析方法研究建筑能耗结果提出建筑改造措施[9]。但目前大多数研究采用的是确定性和局部敏感性分析方法[10, 11],不能全面准确的考虑建筑能耗不确定性,并无法准确提供影响建筑能耗因素的重要性排序。
办公建筑作为公共建筑中典型的建筑类型,具有建筑数量多、使用能耗高的特点。故本文主要选取天津地区办公建筑作为研究对象,采用基于蒙特卡洛抽样的全局敏感性分析和不确定性分析方法,对办公建筑能耗特点进行分析,研究影响办公建筑能耗的主要因素以及办公建筑能耗的概率分布。
1 研究方法
1.1 研究步骤
本研究主要分为五步(如图1所示):第一步首先进行能耗模型的构建,通过确定办公建筑研究参数的分布,并对每个参数在其分布中进行拉丁超立方抽样,得到办公建筑输入参数的组合。然后使用R语言的文字编辑功能,将抽样得到的参数与EnergyPlus构建的基础能耗模型结合,完成能耗模型的构建。第二步运行所得的EnergyPlus办公建筑模型,并通过R语言对建筑能耗模型计算结果进行收集整理。第三步,对于建筑能耗模拟结果进行不确定性分析,得到建筑能耗的均值、偏度、峰度等统计量和概率密度函数等可视化结果。第四步采用树形高斯过程和多元自适应回归样条进行全局敏感性分析。第五步,根据不确定性分析和敏感性分析结果,确定影响建筑办公建筑能耗的关键参数以及能耗分布,并提出优化措施。

图 1 建筑能耗的不确定性及敏感性分析研究流程图
1.2 能耗模型构建
本文选择建立天津地区的办公建筑模型进行建筑能耗计算及分析。为便于模型的建立,所建立的模型建筑的长宽比均为2,建筑的朝向均为北向。建立的办公建筑模型的不确定性参数包括建筑的体形系数、建筑各个方向的窗墙比、窗户的传热系数、太阳得热系数、外墙传热系数、建筑层数、照明功率密度、设备功率密度、人均占有建筑面积以及换气次数等参数,这些参数总结于表1。

表 1 研究选取的不确定性参数变量
由于本文为设计性问题,故表1中参数均服从均匀分布,各个参数的范围按照国标GB 50189–2015《公共建筑节能设计标准》[12]中的规定选取。根GB 50189–2015中的规定,其中窗户的传热系数和太阳得热系数两个参数只有相应的上限值,因此根据查阅相应的文献获得窗户传热系数以及太阳得热系数的下限值。对于换气次数通过查阅相应的文献选取换气次数的范围,具体的参数范围以及参考文献见表1。所建立的建筑模型如图2,需要说明由于建筑的很多参数均为变量,所以图2只是其中的一种参数组合所形成的建筑模型。天津地区绝大多数办公建筑的暖通空调系统为风机盘管[17, 18],因此本文选择风机盘管作为办公建筑的暖通空调系统。使用EnergyPlus进行建筑能耗模拟时需要相应地区的天气数据,本文选择由EnergyPlus提供的天津地区典型年气象数据作为进行建筑能耗计算时的天气数据。

图 2 办公建筑模型示意图
1.3 不确定性分析方法
影响建筑能耗的因素有很多,比如人均占有建筑面积、设备使用时间表、空调设定温度,这些因素都具有很强的不确定性。因此,如何定量化的分析建筑能耗中的这些不确定性因素受到越来越多的关注[2]。不确定性分析方法可以分为两大类:正向不确定性传递和逆向不确定性计算。如果已知建筑中与热性能相关的输入参数,通过建筑能耗模型,得到建筑能耗的概率分布,这属于正向不确定性传递。正向不确定性关注于从输入参数的不确定性通过模型计算量化输出的不确定性。逆向不确定性分析,则是根据建筑能耗实测值和能耗模型,计算建筑能耗模型中的未知参数。正向不确定性的结果可以通过统计量指标或图形进行表示,常用于表示不确定性的统计量指标包括均值,中位数,标准差等,常用于表示不确定性的图形可采用柱状图、箱线图、概率密度函数图以及累计概率密度函数图表示。本文选择正向不确定性分析,通过正向不确定性分析得到天津地区办公建筑能耗分布,并通过相应的方式来表示不确定性分析结果。
1.4 敏感性分析方法
敏感性分析方法已经广泛的应用于建筑能耗分析中[19]。敏感性分析是研究模型中输入变量在其变化范围内变动对输出变量影响大小的分析方法[20]。树形高斯过程是结合了高斯过程和决策树,是一种贝叶斯非平稳和非线性回归模型[21]。根据元模型法的步骤,首先通过树形高斯过程根据输入变量和输出变量建立代理模型,然后使用这个代理模型并结合基于方差的敏感性分析,得到敏感性分析结果。树形高斯过程的敏感性分析结果有主效应和全效应两个指标,主效应和全效应指标的数值越大说明其对结果的影响越大。其中主效应表示各个输入变量单独变化对输出变量的影响,全效应则是考虑了各个变量之间的交互作用之后输入变量对于输出变量的影响。主效应通过计算各输入变量单独作用引起模型输出变量的方差与输出总方差的比值得到的,全效应通过计算各个输入变量及其交互作用引起的模型输出变量的方差与输出总方差的比值得到的。主效应与全效应的差就是输入变量交互作用的影响。具体计算公式为[11]:
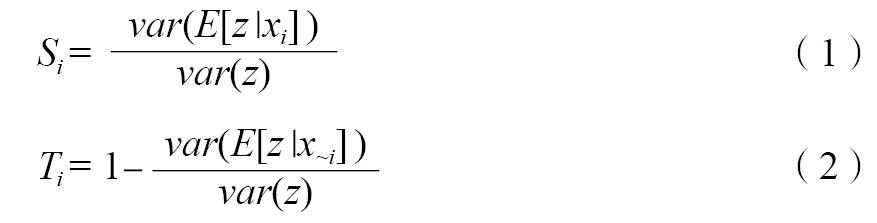
式(1)(2)中:Si 为主效应;Ti 为全效应;xi为输入变量;x~i 为不包括;xi 的其余输入变量;z为模型输出。
2 结果与讨论
2.1 不确定性分析
对于办公建筑取暖能耗不确定性分析结果,从图3中可以得到办公建筑的单位面积取暖能耗的均值为117.21kW·h/m2,中位数为114.18kW·h/m2。单位面积取暖能耗的分布呈现为中间高两边低,即大部分办公建筑的单位面积取暖能耗相差不大,而单位面积取暖能耗过高以及过低的建筑较少,单位面积取暖能耗90%的置信区间为85.35kW·h/m2~153.62kW·h/m2。通过单位面积取暖能耗概率密度图可以得出,概率密度函数的偏度系数为0.53,峰度系数为3.38。
 |  |
| (a)单位面积取暖能耗累积概率密度图 | (b)单位面积取暖能耗概率密度图 |
图3 取暖能耗不确定性分析
对于办公建筑制冷能耗不确定性分析结果,从图4中可以得到办公建筑单位面积制冷能耗的均值为35.98kW·h/m2,中位数为34.81kW·h/m2。单位面积制冷能耗的分布呈现左高右低的趋势,办公建筑单位面积制冷能耗的标准差为7.03,说明办公建筑单位面积制冷能耗较为集中。单位面积制冷能耗的分布比较集中在能耗相对低的范围,即大部分办公建筑的单位面积制冷能耗相差不大,而单位面积制冷能耗过高的建筑较少,单位面积制冷能耗90%的置信区间为27.30kW·h/m2~49.01kW·h/m2。通过单位面积取暖能耗概率密度图可以得出,概率密度函数的偏度系数为0.87,峰度系数为7.04。
 |  |
| (a)单位面积制冷能耗累计概率密度图 | (b)单位面积制冷能耗概率密度图 |
图4 制冷能耗不确定性分析
2.2 敏感性分析
图5表示取暖能耗的全局敏感性分析结果,最重要的三个参数是:人均占有建筑面积、窗户的传热系数以及太阳得热系数。而层数和设备功率密度等对于取暖能耗的影响较小。对于敏感性排序较后的参数则说明其对于取暖能耗的影响较小,在进行办公建筑能耗计算及分析时可适当忽略这些影响较小的参数,主要考虑影响较大的参数来简化能耗计算过程,降低能耗模型的复杂性。
 |  |
| (a)主效应随输入变量的变化 | (b)全效应的变化区间 |
图 5 取暖能耗树形高斯过程敏感性分析
图6表示制冷能耗的全局敏感性分析结果。对于办公建筑制冷能耗影响较大的参数为太阳得热系数以及建筑各个方向的窗墙比。通过敏感性分析结果可以发现,办公建筑窗户的传热系数以及建筑中的人均占有建筑面积与办公建筑制冷能耗的关系为负相关,即窗户的传热系数越大以及人均占有建筑面积越大则建筑的制冷能耗越小。但是,窗户的传热系数以及人均占有建筑面积的变化只能在一定范围内使得制冷能耗有所降低,当窗户的传热系数增加到2W/m2·K以及人均占有建筑面积分别增加9m2/人后,其对于制冷能耗的影响基本不变化。对于人均占有建筑面积而言,一方面随着人均占有建筑面积的持续增加由人散发出的热量就较减少这便会降低建筑的制冷能耗;另一方面风机盘管系统新风量的能耗相比由人产生的能耗要高,所以也会导致这种情况。对于窗户的传热系数而言,如果传热系数过小,则会导致建筑内部的热量不能很好的散失,使得建筑内部的热量都需要空调系统排出,导致增加了建筑的制冷能耗,但如果窗户传热系数的太大,则会导致通过空调系统产生的冷量通过窗户散失出去,增加制冷能耗。
 |  |
| (a)主效应随输入变量的变化 | (b)全效应的变化区间 |
图 6 制冷能耗树形高斯过程敏感性分析
3 结论
通过对办公建筑能耗计算结果的不确定性分析,可以得到通过输入参数不确定性所导致的能耗结果的不确定性,得到办公建筑单位面积取暖能耗、制冷能耗的分布。然后,基于不确定性分析结果,在给定输入参数的条件下来预测建筑能耗。
通过树形高斯过程敏感性分析结果,对于办公建筑取暖能耗而言,对其影响较大的参数主要为人均占有建筑面积,窗户的传热系数以及太阳得热系数。对于办公建筑制冷能耗而言,对其影响较大的参数为太阳得热系数、建筑在各个方向的窗墙比以及窗户的传热系数。对办公建筑能耗进行的敏感性分析,其结果可以帮助新建建筑设计以及既有建筑改造,也可以根据敏感性分析结果把对能耗影响较小的参数删除或者简化考虑,以降低模型的复杂程度以及缩短模型的计算时间。
参考文献
[1] 侯恩哲. 《中国建筑能耗研究报告(2017)》概述[J]. 建筑节能, 2017, (12):131.
[2] Tian W, Heo Y, Wilde P D, et al. A review of uncertainty analysis in building energy assessment[J]. Renewable & Sustainable Energy Reviews, 2018, 93:285–301.
[3] Heo Y, Choudhary R, Augenbroe G A. Calibration of building energy models for retrofit analysis under uncertainty[J]. Energy & Buildings, 2012, 47(4):550–560.
[4] Kristensen M H, Choudhary R, Petersen S. Bayesian calibration of building energy models: Comparison of predictive accuracy using metered utility data of different temporal resolution[J]. Energy Procedia, 2017, 122:277–282.
[5] Hoxha E, Habert G, Lasvaux S, et al. Influence of construction material uncertainties on residential building LCA reliability[J]. Journal of Cleaner Production, 2017, 144:33–47.
[6] Häfliger I-F, John V, Passer A, et al. Buildings environmental impacts’ sensitivity related to LCA modelling choices of construction materials[J]. Journal of Cleaner Production, 2017, 156:805–816.
[7] Rezvan A T, Gharneh N S, Gharehpetian G B. Robust optimization of distributed generation investment in buildings[J]. Energy, 2012, 48(1):455–463.
[8] Shiel P, Tarantino S, Fischer M. Parametric analysis of design stage building energy performance simulation models[J]. Energy and Buildings, 2018, 172:78–93.
[9] Lam J C, Wan K K W, Yang L. Sensitivity analysis and energy conservation measures implications[J]. Energy Conversion & Management, 2008, 49(11):3170–3177.
[10] 王永龙, 潘毅群. 典型办公建筑能耗模型中输入参数单因子敏感性的分析研究[J]. 建筑节能, 2014, (02):9–14.
[11] 何成, 朱丽, 田玮. 城市建筑布局的能耗敏感性分析 [J]. 哈尔滨工业大学学报, 2018, 50:174–180.
[12] 中国建筑科学研究院. 公共建筑节能设计标准:GB50189-2015 [M]. 中国建筑工业出版社, 2015.
[13] 冯雅. 《公共建筑节能设计标准》中外窗及幕墙热工参数的确定 [J]. 暖通空调, 2005, 35:44–47.
[14] 王苏颖, 狄洪发. 窗户太阳得热对严寒地区采暖能耗影响的研究 [C]; 全国暖通空调制冷2002年学术年会, F, 2002.
[15] 张旭, 周翔, 王军. 民用建筑室内设计新风量研究[J]. 暖通空调, 2012, 42(7):27–32.
[16] 孙越霞, 侯静, 张庆男, 等. 天津市居住建筑新风量的测量与分析 [J]. 暖通空调, 2016, 46:10–13.
[17] 李文朝. 天津地区办公建筑节能研究 [D]; 天津大学, 2014.
[18] 陈高峰, 张欢, 由世俊, 等. 天津市办公建筑能耗调研及分析 [J]. 暖通空调, 2012,42:125–128.
[19] Tian W. A review of sensitivity analysis methods in building energy analysis[J]. Renewable & Sustainable Energy Reviews, 2013, 20(4):411–419.
[20] 蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版), 2008, 44(1):9–16.
[21] Gramacy R B, Taddy M. Categorical Inputs, Sensitivity Analysis, Optimization and Importance Tempering with tgp Version 2, an R Package for Treed Gaussian Process Models[J]. Journal of Statistical Software, 2010, 33(i06).
备注:本文收录于《建筑环境与能源》2019年5月刊总第21期。
版权归论文作者所有,任何形式转载请联系作者。









