天津科技大学机械工程学院 田玮 张安朝 朱传琪 史佳鑫
天津市建筑设计院 尹宝泉
摘 要:机器学习可建立计算速度快的建筑能耗统计模型,方便于进行不确定性、敏感性、最优化等研究,机器学习模型精度受很多因素影响,如输入变量数目、抽样方法、样本数量等。本研究重点探究样本数量对机器学习模型预测精度的影响。机器学习方法选取多元自适应回归样条法,以位于天津的办公建筑为例进行研究。结果表明,当建筑能耗分析中样本数量较少时,由于信息缺失导致建筑能耗输入变量间交互作用无法体现。随着样本数量的增加,建筑能耗机器学习模型可以表示出输入变量间的复杂交互作用,并且建筑能耗机器学习模型中所需的项数也增加。研究还发现,样本数量的增加,不仅可提高建筑能耗机器学习模型的预测精度,而且可提高模型预测精度的稳定性。
关键词:机器学习;建筑能耗;样本数量;模型精度
基金项目:国家自然科学基金项目(51778416);教育部哲学社会科学研究重大课题攻关项目(16JZD014)。
0 引言
随着我国建筑能耗的持续增加,为了建立低碳绿色的建筑环境,需要深入了解建筑能耗的特性[1]。时间序列、空间分析、物理模型、统计模型等不同研究方法[2],已经用于解析建筑能耗特点。机器学习做为一种可快速得出能耗计算结果的方法,逐渐在建筑能耗分析中得到广泛应用[3, 4]。常用的机器学习模型包括神经网络(neural network)、支持向量机(support vector machine)、随机森林(random forest)、多元自适应回归样条(multivariate adaptive regression splines,简称MARS)、集成学习(ensemble learning)、深度学习(deep learning)等[5, 6]。田玮等[3]评估了6种不同的机器学习方法,在建筑能耗模型中的适用性。Wei等[4]比较了不同机器学习算法在预测伦敦建筑能耗时的精度。Ngo等[7]比较了不同机器学习方法在预测建筑制冷负荷时的误差。
这些研究对于了解机器学习模型在建筑能耗分析中特点,有非常好的指导作用。但对于样本数量对于机器模型的学习精度没有明确的说明。基于建筑物理模型的机器学习建模,需要一定数量的模型运算得到输入输出数据矩阵。样本数量增多意味着更多的运行时间和成本,所以需要明确样本数量与机器学习模型精度的关系,确定合适的样本数量,以得到准确可靠的机器学习模型。
1 建筑能耗模型
图1为研究中所用的三维建筑能耗模型,这是一个位于天津的L型四层办公建筑。建筑围护结构的热工特性,符合我国2015年发布的公共建筑节能标准[8]。建筑的内部得热,包括人员、设备和照明的得热,与2015年节能标准中附录中的推荐值相同[8]。采用风机盘管系统提供通风、取暖和制冷,建筑有天然气锅炉和风冷式制冷机组提供暖通系统所需的热水和冷水。建筑能耗模拟采用EnergyPlus V9.0程序[9],得到供暖和制冷所需的能耗。

图1 四层办公建筑模型
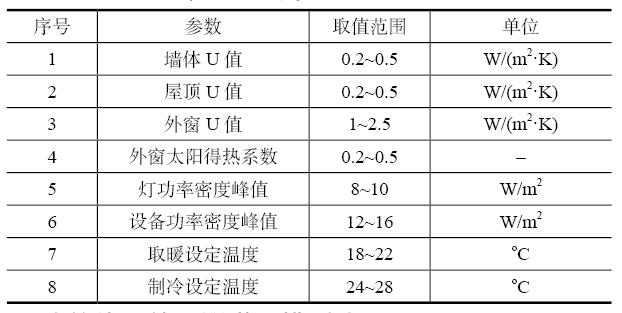
本文研究重点是建立可靠准确的机器学习模型,所以输入参数需要有相应的变化范围,如表1所示。分为3类参数,包括围护结构的热工特性、内部得热和暖通系统参数。围护结构热性能参数包括墙体、屋顶和外窗的总传热系数。内部得热包括照明和设备的功率密度。暖通系统参数包括取暖和制冷的设定温度。由于本文所建立的机器学习模型是为了在这些参数变化范围内得到尽量可靠的模型,所以这些参数假定为均匀分布。采用拉丁超立方法得到这些参数的不同组合,通过建筑能耗计算得到建立机器学习模型所需的数据样本集。拉丁超立方法的特点是良好的分层特性[10],所以可在参数变化的范围内尽量的分布均匀。为了充分研究不同样本数量对于机器学习模型精度的影响,研究中选用40、60、100、200、400、800共6个样本数量。
表1 抽样参数取值范围
2 建筑能耗的机器学习模型建立
机器学习包括很多不同的算法,如随机森林、支持向量机、多元自适应回归样条、神经网络等[11]。研究中选用多元自适应回归样条,是因为先前研究表明这种方法有较高的计算精度,并且有计算速度快的优点。多元自适应回归样条是扩展后的线性模型,可包括非线性和交互作用。在这种机器学习方法中,使用分段后的新变量而不是原始数据集中的变量,所以可表达输入变量和输出变量之间的非线性作用。由于模型结构相对于其它机器学习算法简单,所以方便于分析不同变量间的交互作用,具有较高的模型可解释性。
多元自适应回归样条有两个可调整的参数:模型中变量数目和交互作用阶数。模型中的变量数越多,意味着更为复杂的模型,回归精度会提高,但可能出现过拟,需要采用重抽样方法避免这种过拟[6]。交互作用的阶数为1时,表示模型中变量间不存在交互作用;阶数为2时,表示两个变量间的交互作用;阶数为3时,表示有三个变量间的交互作用。过高的阶数可能导致过拟。所以采用重复交叉验证法,以得到最优的机器学习模型参数,同时避免过拟现象。重复的目的是为减少模型精度估计量的方差,提高模型精度估计的准确程度。模型精度用均方根误差(root mean sequare error, 简称RMSE)表达,RMSE越小表明所得机器学习模型有更高的精度。
3 结果与讨论
本节首先讨论样本数量对机器学习建模过程的影响,然后分析抽样数量对机器学习模型最终优化模型参数的影响,最终确定样本数量对建筑能耗机器学习模型精度及稳定性的影响。
3.1 样本数量对机器学习建模过程的影响
图2表示不同抽样数量对于建筑取暖能耗机器学习模型的影响。当抽样数量为40时,不考虑交互作用模型的精度高于考虑交互作用的模型,表明由于数据过少没有充分的信息可提取,所以无法得出模型中交互作用,最终所得模型为不考虑交互作用的模型,其预测精度也较低。当抽样数量为60时,考虑交互作用与否对最终模型没有影响,其模型预测精度也不高。随着抽样数量增加到200时,由于数据量增加更多的信息可以提取,所以交互作用的模型与不考虑交互作用时相比,有更高的精度。当抽样数量增加到800,与抽样数量为200时的特点基本一致,但模型精度得到进一步提升。因此,足够数量的建筑能耗数据是得到准确机器学习模型的前提。

图2 不同抽样数量对建筑取暖能耗的机器学习建模优化过程影响
图3表示不同抽样数量对建筑制冷能耗机器学习模型的影响。图3表示的规律与图2类似,数据量较小时,由于没有足够的信息,不能体现出变量间复杂的交互作用,其模型预测精度也较低。随着数据样本的增加,可以反应输入变量间的本质关系,所以模型的精度有明显增加,也可以表达变量间的交互作用。

图3 不同抽样数量对建筑制冷能耗的机器学习建模优化过程影响
3.2 样本数量对机器学习模型最终优化参数的影响
图4和图5表示不同抽样数量对建筑取暖能耗机器学习模型最终参数影响的直方图,包括模型中项数和相互作用次数。由图4可以看出,当数据样本数量增大时,模型中的最终项数也增大,表明数据量的增大带来信息量增加,模型需要更多的项数才可以表达输入和输出之间的函数关系。相互作用的次数也有类似关系如图5所示,当抽样数量为40次时,10次重复抽样所得结果的模型都只需要没有交互作用的模型。当抽样数量增加到100次以上时,所有10次重复抽样所得结果都需要二阶交互作用的机器学习模型。

图4 不同抽样数量对建筑取暖能耗机器学习模型中最终项数的影响

图5 不同抽样数量对建筑取暖能耗机器学习模型中交互作用次数的影响
对于不同抽样数量对于建筑制冷模型中最终两个参数的影响,其影响趋势与取暖能耗类似。当抽样数量为40时,制冷能耗机器学习模型有6组抽样只需要11个项。当抽样数量为800时,最少的项数也需要15次,有4组甚至需要17次的项数来表达输入和制冷能耗之间的复杂关系。相互作用阶数也随着抽样数量的增加而增加。
3.3 样本数量对机器学习模型精度的影响
图6表示不同抽样数量对建筑取暖和制冷能耗的影响,包括10次抽样和中位数的结果。对于取暖能耗,当抽样数量从40次增加到60次时,预测精度增加非常明显,RMSE约减少30%。但当样本数量增加到100时,增加幅度就变得非常有限。样本数量400时的精度与样本数量为800时的精度相差很小。当抽样数量从40增加到800时,模型精度的中位数值约增加一半。所以足够数量的样本是机器学习模型精度取得良好效果的前提。在计算机模拟分析中,通常取10倍变量的样本数目,可以得到比较好的精度,但取决于项目的需求,如果对于能耗模型精度有更高要求,则更多的样本数量是必需的。

(a)heating energy (b)cooling energy
图6 不同抽样数量对建筑能耗机器学习模型精度影响
由图6(a)可得出另外一个重要的结论,同样抽样数量的样本,重复抽样所得的结果非常分散。如抽样数量为60所得的结果并不必然比抽样数量为40时,所得结果的误差小。所得机器模型精度的分散程度随着样本数量的增大而减少。所以为了保证模型精度,减少相同样本数量时所得结果的偏差,增大样本数量也非常有必要。
对于制冷能耗的机器学习模型,所得结果与取暖能耗模型类似。模型精度随着样本数量的增加有明显的增加,模型精度随着抽样种子的方差随着样本数量的增加而减少。所以,样本数量的增加不仅可以提高建筑制冷机器学习模型的预测精度,而且也提高了预测精度的稳定性。
4 结语
本研究分析了样本数量对于建筑能耗机器学习模型精度的影响,得出了以下结论:
(1)当建筑能耗分析中样本数量较少时,由于信息缺失导致建筑能耗的输入变量间交互作用无法体现。随着样本数量的增加,建筑能耗机器学习模型可以表示出输入变量间的复杂交互作用。
(2)随着样本数量的增加,建筑能耗机器学习模型中所需的项数也增加,相应模型精度也有一定提升。
(3)建筑能耗分析的样本数量增加,不仅可以提高建筑能耗机器学习模型的预测精度,而且可以提高模型预测精度的稳定性。
因此,建筑能耗分析中样本数量对于机器学习模型精度有明显的影响,样本数量选取需依赖于研究项目的具体目的和要求。如能耗分析人员可根据建筑项目特点,确定机器学习模型精度,在此前提下则可根据交叉验证的结果确定出合适的样本数量。
参考文献
[1] 清华大学建筑节能研究中心. 中国建筑节能年度发展研究报告:2018 [M]. 北京: 中国建筑工业出版社, 2018.
[2] 金涛, 杨小山, 姚灵烨, 等. 城市局地气温对建筑冷负荷的影响 [J]. 建筑科学, 2018,34:32–39.
[3] 田玮, 魏来, 李占勇, 等. 基于机器学习的建筑能耗模型适用性研究 [J]. 天津科技大学学报, 2016:54–59.
[4] Wei L, Tian W, Silva E A, et al. Comparative Study on Machine Learning for Urban Building Energy Analysis[J]. Procedia Engineering, 2015, 121: 285–292.
[5] Amasyali K, El-Gohary N M. A review of data-driven building energy consumption prediction studies[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 1192–1205.
[6] Kuhn M, Johnson K. Applied predictive modeling [M]. Springer, 2013.
[7] Ngo N-T. Early predicting cooling loads for energy-efficient design in office buildings by machine learning[J]. Energy and Buildings, 2019, 182:264–273.
[8] 中国建筑科学研究院. 公共建筑节能设计标准:GB50189-2015 [M]. 中国建筑工业出版社. 2015.
[9] DOE, EnergyPlus V9.0.1, October 2018, Department of Energy, USA [R], 2018.
[10] Tian W, Heo Y, de Wilde P, et al. A review of uncertainty analysis in building energy assessment[J]. Renewable and Sustainable Energy Reviews, 2018, 93:285–301.
[11] Wei Y, Zhang X, Shi Y, et al. A review of data-driven approaches for prediction and classification of building energy consumption[J]. Renewable and Sustainable Energy Reviews, 2018, 82:1027–1047.
备注:本文收录于《建筑环境与能源》2019年5月刊总第21期。
版权归论文作者所有,任何形式转载请联系作者。









